| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- weighted least-squares
- 변수분리#동차 미분방정식#완전 미분방정식
- 푸리에 정리
- linespectra#feurierseries#푸리에 급수
- reflection matrix
- 여인수 행렬
- 오일러-코시 미방#계수내림법
- 내적#duality#쌍대성#dot product
- 내적 공간#적분
- 베르누이 미분방정식
- 부분 분수분해
- 선형시스템연산자#라이프니츠 법칙#fundamental theorem of algebra#erf
- 멱급수법
- 선형변환#contraction#expansions#shears#projections#reflection
- 정규직교행렬
- 2계미방#모드#mod#특성방정식#characteristic eq#제차해
- 여인자
- 계수내림법#reduction of order#wronskian#론스키안#아벨항등식#abel's identity
- 상태천이행렬#적분인자법#미정계수법#케일리-헤밀톤 정리
- 직교행렬#정규직교행렬#orthonormal#reflection matrix#dcm
- 선형독립#기저벡터#선형확장#span#basis
- 비제차#제차해#일반해#적분인자#적분인자법#homogeneous sol#nonhomogeneous sol#integrating factor
- 미분방정식 #선형 미분방정식 #상미분 방정식
- 푸리에 급수
- 가중 최소제곱법
- 추정문제#normal equation#직교방정식#정사영#정사영행렬#정사영 변환
- 최소자승#least-square#목적함수#양한정#정점조건#최소조건
- dirichlet
- 그람-슈미트 과정#gram-schmidt process
- 선형 상수계수 미분방정식#lccode#sinusoidal input
OnlyOne
합성곱, 임펄스 응답(Convolution Theorem; Impulse Response) 본문
합성곱, 임펄스 응답(Convolution Theorem; Impulse Response)
Taesan Kim 2024. 8. 21. 07:46합성곱, 임펄스 응답(Convolution Theorem; Impulse Response)
Intro
오늘 포스팅을 관통하는 핵심 문장이 있다.
System's zero-state response can be determined from known input-output pair
즉, 입출력 한쌍만 알고 있어도 다른 모든 입력에 의한 출력을 알 수 있다는 의미이다.
Convolution Theorem

합성곱(Convolution)은 디락델타 신호를 Shifting 하여 각 위치에서의 함숫값을 곱하고 모두 더해주는 계산이다. 위 계산이 어떻게 나왔는지는 아래 그림을 보면 이해가 잘 갈 것이다.
By the quadrature rule, the arbitrary input signal can be approximated as a linear combination of rectangular pulses

위 그림은 Rectangular pulse를 이용하여 f를 근사하는 식이다. Rectangular pulse를 Shifting하여 무수히 더한 것이 보이는가? 위 식을 합성곱 식이 되게하기 위해 다음과 같은 계산을 거친다.

단순한 적분계산을 통해 우리는 합성곱의 유래를 이해할 수 있다.
Causal LTI System
우리가 분석하는 시스템은 LTI시스템이므로, 0 이전에 Input값은 모두 0이다. 이를 이용하면 합성곱 식을 더 간단히 정리할 수 있다. 정리식은 다음과 같다.
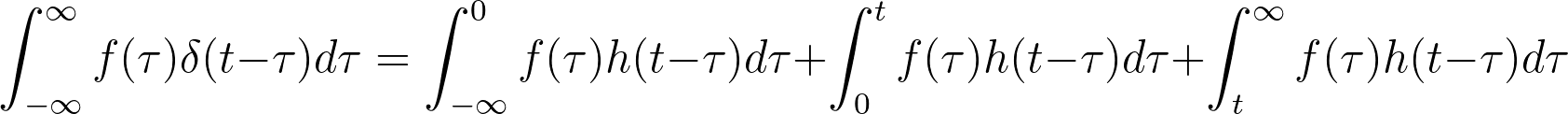
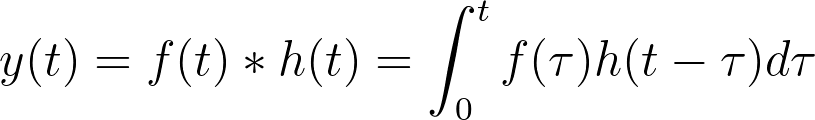
Impulse Response
맨 처음에 Known Input Output Response를 기억하는가? 만약 I/O쌍이 Impulse Response라면 모든 y를 알 수 있다. 그럼 Impulse Response란 무엇일까? 차근차근 보자.
시스템에 입력으로 Impulse Delta Signal을 넣었다고 가정하자. 그때 결과로 나오는 식이 Impulse Response이다. 우리는 Impulse Response 하나만 가지고 시스템의 모든 입출력을 알 수 있다. y의 값을 다음과 같이 분석할 수 있기 때문이다.

결론적으로, y(t)는 f를 입력이라고 할 때, 항상 다음과 같은 식을 만족시킨다.

Q. 어떻게 h(t)를 구할까?
- Unit Step 신호의 결과값을 미분한다.(사실상 이 방법은 노이즈가 반드시 발생하는 현실에서 쓸모없다. 미분은 노이즈를 증폭시키는 효과가 있기 때문이다.)
- 대놓고 계산하는 방법도 있다. 이 방법으로 밑에 예제를 풀도록 하겠다.(글로 하자면 길기 때문이다.)
Exercise
다음 시스템의 임펄스 응답을 구하여라.

해설은 다음과 같다.

Conclusion
Impulse Response h(t)는 시스템의 고유한 특성을 담고 있다. 우리는 Impulse Response를 통해 모든 Zero-State Response를 예측할 수 있다. 또한 시간 영역 시스템 모델에서 입출력 결정을 위한 가장 기본적인 정보를 제공하는 역할을 하기도 한다. Impulse Response는 미분방정식에서 homogeneous solution과 같다. 결국 homogeneous Solution이 모든 것을 결정한다.
2024.08.21 - [Engineering/Linear System and Signal] - 시스템 응답(System response)[0]
시스템 응답(System response)
시스템 응답(System response) Intro오늘은 LTI시스템의 분석에서 LTI시스템의 응답 분석의 개요를 설명할 것이다. Zero State Response, Zero Input ResponseLTI시스템은 LCCODE(Linear Constant Coefficient Ordinary Differenti
taesan5435.tistory.com
'Control Engineering > Linear System and Signal' 카테고리의 다른 글
| MAF(Moving Average Filter) (0) | 2024.08.24 |
|---|---|
| 푸리에 급수, Line Spectra(Feurier Series; Line Spectra) (0) | 2024.08.23 |
| 비선형 시스템의 선형화(Linearization of Nonlinear system) (0) | 2024.08.19 |
| 시스템(System) (1) | 2024.08.19 |
| Dominant Pole Concept (0) | 2024.08.16 |




