| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 내적#duality#쌍대성#dot product
- 부분 분수분해
- 2계미방#모드#mod#특성방정식#characteristic eq#제차해
- 비제차#제차해#일반해#적분인자#적분인자법#homogeneous sol#nonhomogeneous sol#integrating factor
- 푸리에 정리
- 추정문제#normal equation#직교방정식#정사영#정사영행렬#정사영 변환
- 멱급수법
- 베르누이 미분방정식
- 선형시스템연산자#라이프니츠 법칙#fundamental theorem of algebra#erf
- 푸리에 급수
- 직교행렬#정규직교행렬#orthonormal#reflection matrix#dcm
- weighted least-squares
- 내적 공간#적분
- 그람-슈미트 과정#gram-schmidt process
- 여인수 행렬
- dirichlet
- 오일러-코시 미방#계수내림법
- 선형변환#contraction#expansions#shears#projections#reflection
- linespectra#feurierseries#푸리에 급수
- 선형 상수계수 미분방정식#lccode#sinusoidal input
- 계수내림법#reduction of order#wronskian#론스키안#아벨항등식#abel's identity
- 선형독립#기저벡터#선형확장#span#basis
- 여인자
- 미분방정식 #선형 미분방정식 #상미분 방정식
- 정규직교행렬
- 가중 최소제곱법
- reflection matrix
- 변수분리#동차 미분방정식#완전 미분방정식
- 최소자승#least-square#목적함수#양한정#정점조건#최소조건
- 상태천이행렬#적분인자법#미정계수법#케일리-헤밀톤 정리
OnlyOne
테일러 급수와 테일러 정리(Taylor Series) 본문
테일러 급수와 테일러 정리(Taylor Series)
테일러 급수란, 한 점 C부근에서 f(x)와 비슷한 함숫값을 구하기 위한 무한 차수 근사식과 같다.
Q. 우리는 e^(0.1)값을 어떻게 계산할 수 있을까?
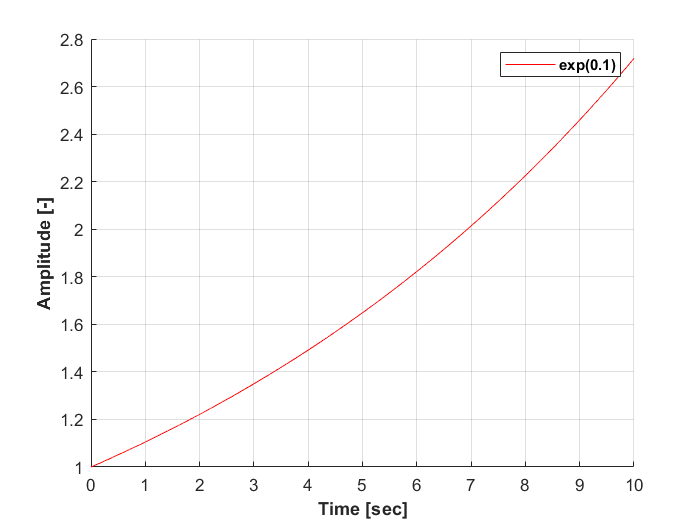
Q. X=0주변에서 e^x와 비슷한 함숫값을 갖는 다항식을 어떻게 찾을까?
이 질문은 "비선형 함수를 어떻게 선형적으로 나타낼 것인가?" 하는 질문과 밀접한 관련이 있으며, 제어공학에서 비선형 신호를 선형 신호로 변환하여 선형시스템에서 신호를 처리하므로, 제어공학적 관점에서도 매우 중요하다.
첫번째 질문에 대한 답은 간단하다. 미분을 이용하는 것이다.
1계 미분을 통해 x=0일 때, e^x접선은 x+1이고, 따라서 e^(0.1) ≒ 1 + 0.1 = 1.1로 근사가 가능하다.
Q. 그렇다면 오차 e^0.1 - 1.1은 얼마나 될까?
이 질문에 대답하기 위해서 우리는 테일러 급수를 이해해야 한다.
테일러 급수(Taylor Series)와 매클로린 급수
테일러 급수란, 한 점 C부근에서 f(x)와 비슷한 함숫값을 구하기 위한 무한 차수 근사식과 같다.
: 이때, C는 Center이고, Center이 0이면 매클로린 급수이다.
테일러 급수의 이해

테일러 급수를 수식으로 표현하면 다음과 같다.
이때 주의해야 할 것은 위 식은 X=a 근처에서만 성립하는 식이며 a에 대한 n차 근사식이라고 표현한다는 점이다.
즉, X=a점에서 멀어질수록 오차가 커진다. 이때 a를 center이라고 한다. 오차범위의 중심에 위치해있기 때문인 듯 싶다..
이제 우리는 테일러 급수를 이용하여 f의 n차 근사식을 구할 수 있다!
테일러 정리(Taylor's Theorem)
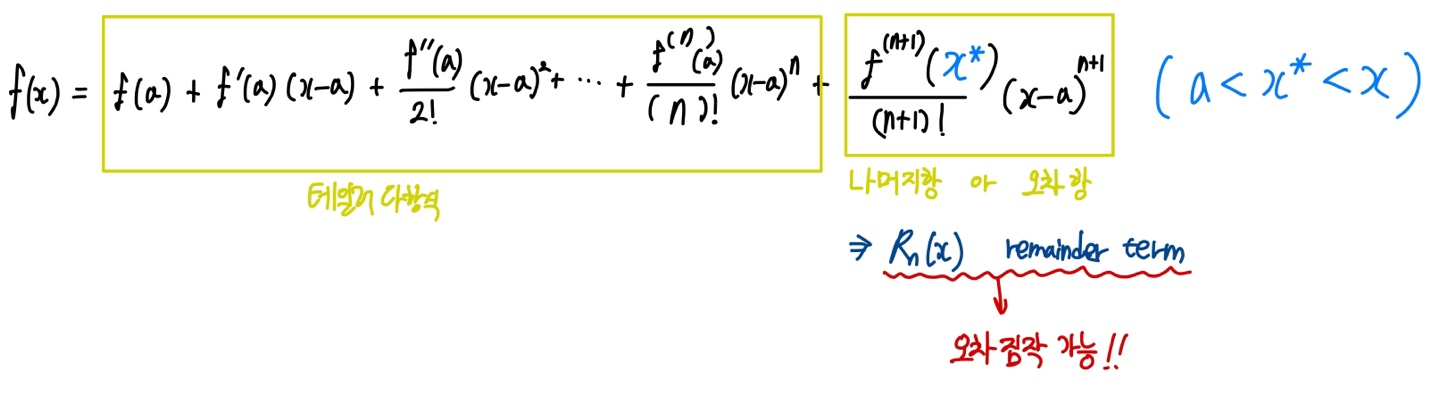
테일러 정리의 정의는 다음과 같다. 테일러 급수에 오차를 구하는 항(Remainder term) 하나가 더 붙은 형태이다. 이때 X스타는 a와 x사이의 범위, 즉 오차범위를 의미한다. 이 추가적인 장치를 통해 오차를 짐작할 수 있다.
테일러 전개식 = 테일러 다항식 + Remainder term
예제





테일러 급수는 오일러 공식을 유도하는데 쓰이곤 한다. 관련 포스팅을 올려놓았다.
2024.08.12 - [Engineering/Linear System and Signal] - 오일러 공식[Euler Formula]
오일러 공식[Euler Formula]
오일러 공식[Euler Formula]모든 Exponential function은 Sinusoidal function으로 분해할 수 있다. 이러한 특성으로 인해 푸리에 변환에서 Exponential function은 기저함수(Basis function)으로 기능하기도 한다. 오늘
taesan5435.tistory.com
마치며...
다변수함수의 테일러 정리를 후에 다루도록 하겠다. 많관부
2024.08.18 - [Mathematics/Calculus] - 테일러 정리(Taylor's theorem)
테일러 정리(Taylor's theorem)
테일러 정리(Taylor's theorem)테일러 정리가 돌아돌아돌아왔다. 오늘은 이전에 배운 테일러 급수와 테일러 정리의 확장판이다. 다변수함수에서 테일러 정리를 적용하는 법을 배운다. 테일러 정리
taesan5435.tistory.com
'Mathematics > Vector Calculus' 카테고리의 다른 글
| 연쇄법칙과 음함수 정리(Chain Rule and Implicit Function Theorem) (1) | 2024.08.16 |
|---|---|
| 방향미분(Directional derivative) (0) | 2024.08.15 |
| 기울기벡터와 접평면(Gradient & Tangent plane) (0) | 2024.08.15 |
| 편미분(partial derivative)과 편도함수 (0) | 2024.08.14 |
| 다변수 함수 (0) | 2024.08.11 |




