| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 베르누이 미분방정식
- 선형변환#contraction#expansions#shears#projections#reflection
- 푸리에 급수
- 계수내림법#reduction of order#wronskian#론스키안#아벨항등식#abel's identity
- linespectra#feurierseries#푸리에 급수
- 추정문제#normal equation#직교방정식#정사영#정사영행렬#정사영 변환
- 최소자승#least-square#목적함수#양한정#정점조건#최소조건
- 직교행렬#정규직교행렬#orthonormal#reflection matrix#dcm
- 가중 최소제곱법
- 미분방정식 #선형 미분방정식 #상미분 방정식
- 푸리에 정리
- 변수분리#동차 미분방정식#완전 미분방정식
- 내적#duality#쌍대성#dot product
- 오일러-코시 미방#계수내림법
- 멱급수법
- dirichlet
- 상태천이행렬#적분인자법#미정계수법#케일리-헤밀톤 정리
- weighted least-squares
- reflection matrix
- 그람-슈미트 과정#gram-schmidt process
- 내적 공간#적분
- 비제차#제차해#일반해#적분인자#적분인자법#homogeneous sol#nonhomogeneous sol#integrating factor
- 여인자
- 부분 분수분해
- 선형 상수계수 미분방정식#lccode#sinusoidal input
- 선형독립#기저벡터#선형확장#span#basis
- 정규직교행렬
- 여인수 행렬
- 2계미방#모드#mod#특성방정식#characteristic eq#제차해
- 선형시스템연산자#라이프니츠 법칙#fundamental theorem of algebra#erf
OnlyOne
라플라스 변환, ROC, 부분 분수분해(Laplace Transform; Region of Convergence; Partial Fraction Expansion) 본문
라플라스 변환, ROC, 부분 분수분해(Laplace Transform; Region of Convergence; Partial Fraction Expansion)
Taesan Kim 2025. 3. 28. 05:18라플라스 변환, ROC, 부분 분수분해(Laplace Transform; Region of Convergence; Partial Fraction Expansion)
라플라스 변환을 시스템 해석에 사용하는 이유는 무엇인가?
들어가며...
라플라스 변환은 개념 자체가 담고 있는 의미가 많고 내용도 많기 때문에(필자에게는 그렇게 느껴진다.) 이번 포스팅에서는 최대한 기본 개념과 계산적인 측면에서 정리할 것이다. 라플라스 변환의 공식 증명, 라플라스 역변환 직접 적분과 같은 내용은 살짝 언급만 하고 굳이 여기서 다루지는 않을 것이다.
라플라스 변환
라플라스 변환이 나오게 된 배경은 선형 시스템과 신호 과목에서 깊이있게 다루고 있는 부분이다. 간단히 짚고 넘어가자면, 원래 주기함수에만 적용 가능했던 푸리에 급수를 비주기함수에도 적용하기 위해 주기를 무한대로 보냄으로써 수정된 푸리에 급수 즉, 푸리에 변환이 고안되었다.
그러나, 푸리에 변환도 발산하는 함수를 다루지는 못하는 문제가 있었다. 이를 해결하기 위해 기저함수에 시스템의 안정성을 결정하는 '시그마'를 추가하여 시그마가 특정 범위에 있을 때, 발산하는 함수를 처리할 수 있는 방법이 고안되었다. 이 방법이 바로 라플라스 변환이다.

여기서 s는 복소수이며, 아래와 같이 표현할 수 있다.

라플라스 변환은 시간 영역에서 정의된 함수 f(t)를 s-평면 상에서 정의된 함수 F(s)로 매핑한다.

위 영역을 라플라스 영역이라 하며, s-평면을 복소 평면이라 한다.
라플라스 변환은 위 식의 우변이 수렴하게 하는 s에 대해서만 정의되기 때문에, 시그마의 값에 따라 라플라스 변환이 정의되는 구간이 결정된다. 이를 식으로 표현하면 아래와 같다.


ROC(Region of Convergence)
라플라스 변환이 정의되도록 하는 s의 범위를 수렴구간이라 하여 ROC라 한다. ROC는 복소 좌표계인 s-평면 상에서 정의된다.

예를 들어 f가 아래와 같다고 해보자.

수렴조건을 계산하면 아래와 같다.
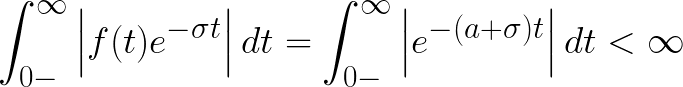

만약 a가 음수라면, ROC는 s-평면의 우반면에 위치할 것이고, 만약 a가 양수라면, ROC는 s-평면의 일부 좌반면도 포함할 것이다.
라플라스 역변환
라플라스 역변환은 s-평면 상의 contour 적분으로 정의된다. 수학적으로 아래와 같이 표현된다.

직접 적분을 하는 경우에 그린 정리가 사용되며 복소해석학에서 다루는 contour적분이 사용되기 때문에 계산이 상당히 복잡하다. 하지만, 많은 경우 직접 적분보다는 부분 분수분해(PFE: partial fraction expansion)와 사전에 정리해 둔 주요 함수들에 대한 라플라스 변환 공식을 사용하여 문제를 해결한다.
PFE(partial fraction expansion)
부분 분수분해는 라플라스 변환과 역변환이 적분 형태로 정의되어 선형성을 만족한다는 점에서 착안된 해법이다. 부분 분수분해는 아래와 같은 식으로 표현한다. 여기서 F(s)는 s에 대한 유리함수이며, n은 m보다 크거나 같다.


라플라스 변환 테이블
증명은 이번 포스팅에서 다루지 않고, 자동제어 카테고리에서 다룰 예정이다.


Example
아래와 같은 유리함수로 정의된 F(s)를 라플라스 역변환을 해보자.

양변에 s+2를 곱하고 s = -2를 대입하면 k1 = 1/9가 나온다. 같은 방법으로 r2를 1/3으로 구할 수 있다. r1을 구하기 위해서 위 식을 s에 대해 한번 미분해주면 된다. 미분하면 아래 식과 같다.
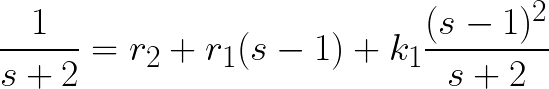

따라서 r1은 -1/9가 된다. 결과적으로 식은 아래와 같이 표현 가능하다.

라플라스 역변환 공식을 적용하면 아래와 같은 결과가 나온다.

마치며...
이번 포스팅은 라플라스 변환과 그와 관련된 기본 개념들을 살펴보았다. 라플라스 변환은 미분방정식을 주파수 영역에서 분석하여 문제를 해결한다는 점에서 시간 영역에서 해석하기 어려운 시스템을 이해하는데 강력한 도구로 작용한다. 특히 단순한 대수 연산으로 해를 구할 수 있는 점은 라플라스 변환의 가장 매력적인 특징이다.
라플라스 변환의 이러한 특징은 미분방정식 형태로 모델링된 시스템을 해석하고 제어하는 제어공학에 많은 기여를 하고 있다. 자동제어 카테고리에서 라플라스 변환을 시스템 해석적인 측면에서 살펴보도록 하겠다.
읽어주셔서 감사합니다.
'Mathematics > Differential Equation' 카테고리의 다른 글
| 푸리에 급수, 시스템 해석(Fourier Series; System analysis) (0) | 2025.03.26 |
|---|---|
| 푸리에 정리, 푸리에 급수, 디리클레 조건(Fourier Theorem; Fourier Series; Dirichlet Conditions) (0) | 2025.03.26 |
| 오일러-코시 방정식(Euler-Cauchy Equation) (0) | 2025.03.22 |
| 멱급수법(Power Series Method) (0) | 2025.03.21 |
| 계수 내림법, 론스키안, 아벨 항등식(Reduction of Order; Wronskian; Abel's identity) (0) | 2025.03.21 |





