| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 멱급수법
- 선형 상수계수 미분방정식#lccode#sinusoidal input
- 베르누이 미분방정식
- reflection matrix
- 정규직교행렬
- 내적#duality#쌍대성#dot product
- 계수내림법#reduction of order#wronskian#론스키안#아벨항등식#abel's identity
- 푸리에 급수
- 그람-슈미트 과정#gram-schmidt process
- 오일러-코시 미방#계수내림법
- 푸리에 정리
- 미분방정식 #선형 미분방정식 #상미분 방정식
- 선형독립#기저벡터#선형확장#span#basis
- 최소자승#least-square#목적함수#양한정#정점조건#최소조건
- 여인자
- 여인수 행렬
- 상태천이행렬#적분인자법#미정계수법#케일리-헤밀톤 정리
- 선형시스템연산자#라이프니츠 법칙#fundamental theorem of algebra#erf
- 2계미방#모드#mod#특성방정식#characteristic eq#제차해
- 비제차#제차해#일반해#적분인자#적분인자법#homogeneous sol#nonhomogeneous sol#integrating factor
- 가중 최소제곱법
- 부분 분수분해
- 직교행렬#정규직교행렬#orthonormal#reflection matrix#dcm
- dirichlet
- 변수분리#동차 미분방정식#완전 미분방정식
- 추정문제#normal equation#직교방정식#정사영#정사영행렬#정사영 변환
- 선형변환#contraction#expansions#shears#projections#reflection
- weighted least-squares
- 내적 공간#적분
- linespectra#feurierseries#푸리에 급수
OnlyOne
Linear Transformation; 선형변환의 정의 본문
Linear Transformation; 선형변환의 정의
들어가며...
흔히 선형변환 T = Ax로 정의한다. 그렇다면 A는 어디서 왔고, T는 어디서 왔을까?
Linear Transformation T
크기(size)가 2×2인 단위행렬(identity matrix)을 가정한다고 했을 때 그 단위행렬은 아래와 같이 두 elementary matrix의 합으로 표현할 수 있다.
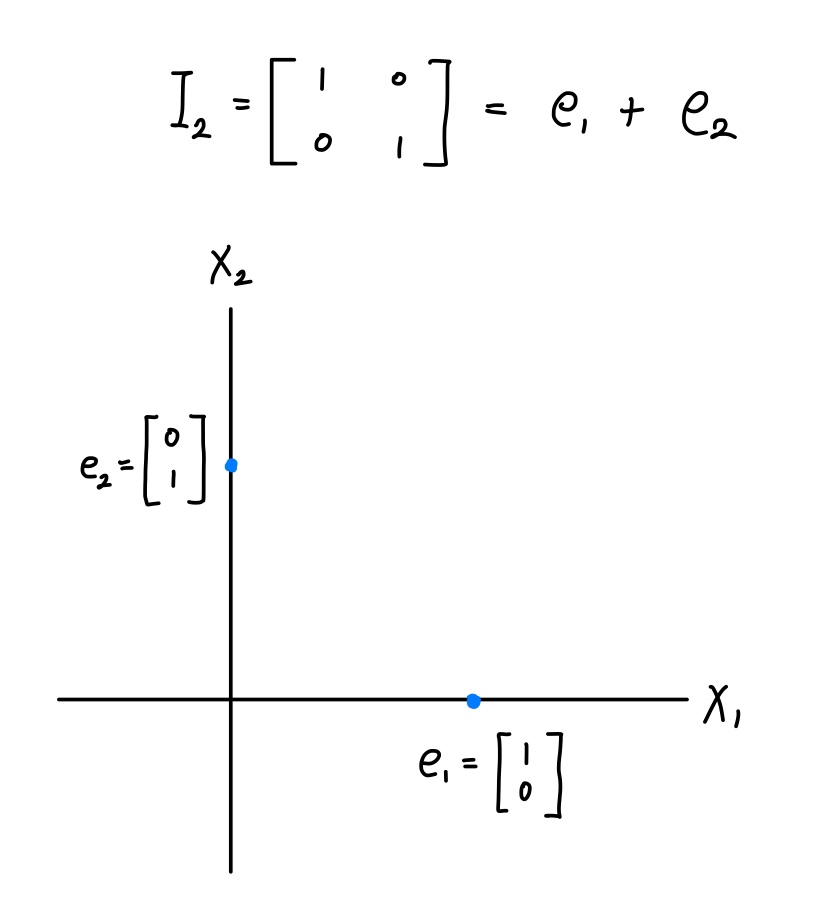
차원을 2차원에서 3차원으로 변환시켜주는 선형변환 T라고 하고, 이때
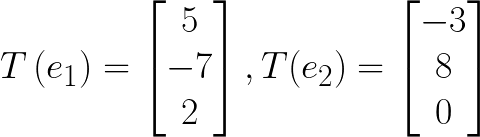
이라 가정한다.
이때 X를 다음과 같이 표현할 수 있다.
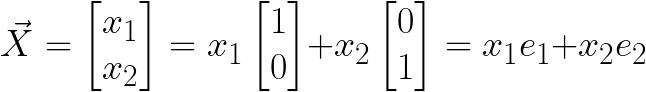
이 식을 이용하면 다음과 같이 T(X)를 표현할 수 있다.
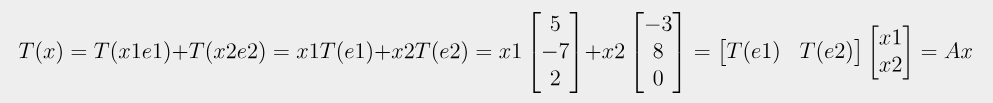
여기서 A가 파생되며, 이때 A의 size는 3×2이다. 만약 A라는 행렬이 n차원을 m차원으로 변환하는 선형변환 T에 대한 행렬이라면, A의 Size는 m×n이 되는 것이다.
A를 수학적으로 Standard matrix for the Linear Transformation T 라고 정의하며, 그 수식은 다음과 같다.

Q. 선형변환을 하는 이유는 무엇일까?
이미 유추했겠지만, 선형변환을 하는 본질적인 이유는 벡터의 크기를 조절(Scaling)하거나, 방향을 바꾸기(Rotating) 위함이다.
우리는 Scaling을 하는 과정에서 우리의 예상보다 더 많은 결과로서의 선형변환을 할 수 있다.
선형 변환에 대한 구체적인 사례들은 다음 포스팅을 참고하길 바란다.
2024.07.30 - [Mathematics/Linear Algebra] - Linear Transformation; 선형변환의 활용
Linear Transformation; 선형변환의 활용
선형대수학[Linear Transformation; 선형변환의 활용]이전 포스팅에서 다루었던 주제인 선형변환의 예제를 푸는 시간을 갖도록 하겠다. 2024.07.30 - [수학 이야기] - 선형대수학[Linear Transformation; 선
taesan5435.tistory.com
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 동차 좌표계(Homogeneous Coordinates) (0) | 2024.07.31 |
|---|---|
| Linear Transformation; 선형변환의 활용 (0) | 2024.07.30 |
| 일대일(one-to-one), 일대일 대응, 전사(injective), 단사(surjective) (0) | 2024.07.29 |
| 선형성이란?(Superposition, Homogeneity, Additivity) (0) | 2024.07.29 |
| 동차해&특수해&일반해(Homogeneous solution&Particular solution&General solution) (0) | 2024.06.22 |




