| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 내적#duality#쌍대성#dot product
- 푸리에 급수
- 여인자
- 푸리에 정리
- 선형독립#기저벡터#선형확장#span#basis
- dirichlet
- 오일러-코시 미방#계수내림법
- 내적 공간#적분
- 비제차#제차해#일반해#적분인자#적분인자법#homogeneous sol#nonhomogeneous sol#integrating factor
- 변수분리#동차 미분방정식#완전 미분방정식
- 최소자승#least-square#목적함수#양한정#정점조건#최소조건
- 선형변환#contraction#expansions#shears#projections#reflection
- weighted least-squares
- 여인수 행렬
- 정규직교행렬
- 미분방정식 #선형 미분방정식 #상미분 방정식
- reflection matrix
- 부분 분수분해
- 선형시스템연산자#라이프니츠 법칙#fundamental theorem of algebra#erf
- linespectra#feurierseries#푸리에 급수
- 상태천이행렬#적분인자법#미정계수법#케일리-헤밀톤 정리
- 계수내림법#reduction of order#wronskian#론스키안#아벨항등식#abel's identity
- 선형 상수계수 미분방정식#lccode#sinusoidal input
- 멱급수법
- 2계미방#모드#mod#특성방정식#characteristic eq#제차해
- 추정문제#normal equation#직교방정식#정사영#정사영행렬#정사영 변환
- 가중 최소제곱법
- 직교행렬#정규직교행렬#orthonormal#reflection matrix#dcm
- 그람-슈미트 과정#gram-schmidt process
- 베르누이 미분방정식
OnlyOne
직교행렬, 정규직교행렬(Orthogonal matrix; Orthonormal matrix) 본문
직교행렬, 정규직교행렬(Orthogonal matrix; Orthonormal matrix)
Taesan Kim 2025. 3. 7. 20:01직교행렬, 정규직교행렬(Orthogonal matrix; Orthonormal matrix)
어떤 기저벡터를 택할 때 벡터연산이 편리한가?
들어가며...
기저벡터 개념을 통해 벡터공간을 나타내는 기저벡터의 경우의 수는 무수히 많음을 알 수 있다. 하지만, 어떤 기저벡터는 다른 기저벡터보다 연산이 매우 용이하다. 오늘은 정규직교행렬의 개념과 그에 관한 예시인 좌표변환행렬과 Reflection matrix를 살펴볼 것이다.
정규직교행렬(Orthonormal matrix)
크기가 1인 행벡터들로 이루어진 직교행렬을 의미한다. 정규직교행렬은 다음과 같은 특징이 있다.

정규직교행렬은 역변환이 굉장히 쉽다는 장점이 있다.

좌표변환행렬(Rotation Matrix); DCM(direction cosine matrix)
좌표변환행렬은 벡터의 방향과 크기를 바꾸지 못한다. 그저 좌표계를 변환할 뿐이다.

위 좌표변환행렬에 의해 Z축에 대해 데카르트 좌표계가 회전한다. 위 변환을 수행하는 좌표변환행렬은 아래와 같다.

좌표변환행렬은 물리적 특성 상, 항상 역행렬이 존재하며, 각 열벡터의 크기가 1이므로, 좌표변환행렬은 단위직교행렬임을 알 수 있다. 따라서, transpose를 이용하여 역행렬을 손쉽게 계산할 수 있다.

좌표변환행렬의 또 하나의 두드러진 특징은 행렬식이 1이라는 점이다. 이는 좌표변환 이후에도 벡터공간의 볼륨변화가 없다는 것을 의미한다.

Reflection Matrix
반사 기준선에서 수직인 벡터와 반사의 대상이 되는 벡터가 주어질 때, 반사된 벡터를 알려주는 변환을 Reflection Matrix라 한다.
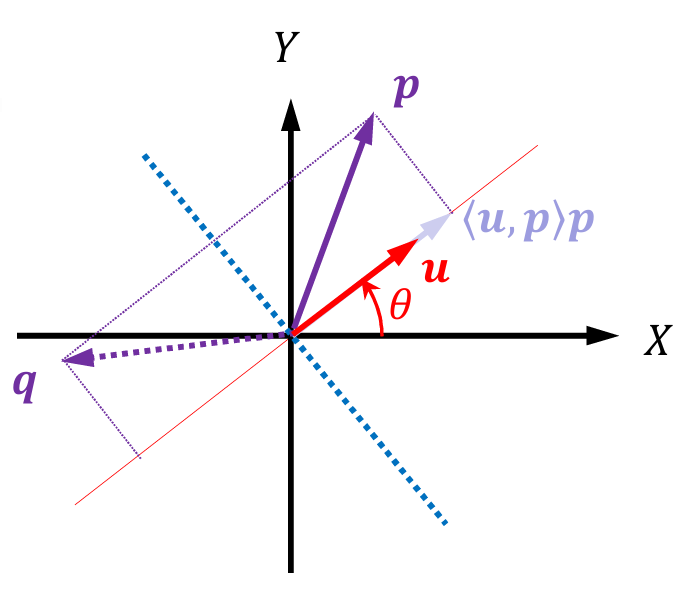

p벡터에 특정 행렬을 곱해서 q벡터를 구하기 위해서, u방향에 대한 p벡터의 정사영 벡터를 p벡터에서 2번 빼주면 된다. 이때, 내적의 물리적 의미는 정사영 길이와 그 대상이 되는 벡터를 곱한 값이므로, p와 u의 내적에 u벡터를 한 번 곱해주면 u방향에 대한 p벡터의 정사영 벡터를 알 수 있다.(u벡터는 크기가 1인 벡터이므로.)

따라서 Reflection Matrix는 다음과 같이 정의된다.

그럼 Reflection Matrix가 정규직교행렬인지 확인해보자.
1. 대칭행렬
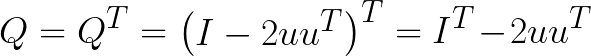
2. 직교행렬

Reflection Matrix가 정규직교행렬임을 알 수 있다. 따라서 Reflection Matrix로 변환된 벡터의 크기에 변화가 없음을 알 수 있으며, 이는 Q를 이용한 변환은 기저 변환에 의한 좌표 변환에 불과하기 때문이다.
마치며...
Reflection matrix는 향후 수치해석에서 역행렬을 구하는데 이용되는 Householder matrix에 사용되는 개념이므로, 기억해두는 것이 좋다. 긴 글 읽어주셔서 감사합니다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 추정문제, 정사영, 정사영 행렬(Estimation; projection; projection matrix) (0) | 2025.03.12 |
|---|---|
| 행렬식(Determinant), 여인자(cofactor), 외적(Cross-product) (0) | 2025.03.08 |
| 열공간, 영공간, 행공간(Column space; Null space; Row space) (0) | 2025.03.04 |
| 벡터공간, 부분공간(vector space, subspace), Rank (0) | 2025.03.04 |
| 공간과 차원(Space&Dimension) (0) | 2025.03.03 |




