Numerical Solution Error and Taylor Series

Numerical Solution Error and Taylor Series

 

Intro

Numerical method is processed in a digital system such as PC or MCU. The main problem of numerical method is that it can produce errors due to limited number of digits representing numbers, chopping, round-off, and truncation errors. We will analyze the total error of the numerical solution.

 

Representation of Error

Absolute total error:

Absolute Error = |True Value - Numerical Solution|

 

We need to be careful how to interpret the absolute error. For example, assume that we have obtained the solution with the true error of 1mm. Can we say this is an accurate solution? -> Compare the absolute error of '1mm' from measuring a length of 10mm vs 1000mm

 

Relative total error

 

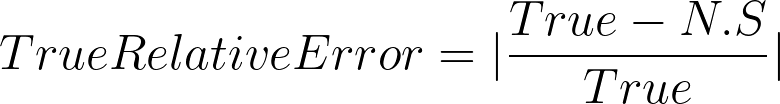
This is non-dimensional and scale-independent. 

In general, the true value is not known when solving numerical problems. Others means are used to evaluate the error or the accuracy, such as estimating the error bounds and approximating order of magnitude of errors.

 

Accuracy vs Precision

Accuracy: How close is the data to the target value?

Precision: Density of data

 

 

Total Numerical Error

Total error = Truncation error + Round-off error

The total error of the numerical solution is a combination of various errors.

 

Round-off error

The round-off error is caused by the limitation of bit count. The limitation of bit count causes underflow(the smallest number closest to zero cannot defined.), overflow, chopping(truncating repeating decimals), and rounding

 

Truncation error

It occurs when numerical method use approximate mathematical procedure.

For example, Taylor series.

 

2024.08.02 - [Mathematics/Calculus] - 테일러 급수와 테일러 정리(Taylor Series)

테일러 급수와 테일러 정리(Taylor Series)

 

Taylor Series practice

Header file

/*
====================================================
Handong Global University
----------------------------------------------------
Name:		Taesan Kim
ID:			22300203
Create:		2024.09.05
Modifier:	2024.09.05
----------------------------------------------------
Approximation of sinusoidal and exponential function
====================================================
*/
#pragma once
#ifndef		_MY_NP_H
#define		_MY_NP_H

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

extern void printVec(double* vec, int row);

#define		PI		3.14159265358979323846264338327950288419716939937510582

//x factorial
double factorial(int _x);

//approximation of sin in rad
double sinTaylor(double _x);

//approximation of sin in deg
double sindTaylor(double _x);

//approximation of cos in rad
double cosTaylor(double _x);

//approximation of exp in rad
double expTaylor(double _x);

// degree to radian
double deg2rad(double _x);

//power x^N
double power(double _x, int N);

#endif

 

 

Source file

#include "myNP_tutorial.h"

void printVec(double* vec, int size)
{
	for (int i = 0; i < size; i++)
		printf("Vector[%d] = %.1f \n", i, vec[i]);
	printf("\n");
}

// factorial function
double factorial(int N)
{
	int y = 1;
	for (int k = 2; k <= N; k++)
		y = y * k;

	return y;
}


//  Taylor series approximation for sin(x) (input unit: [rad])
double sinTaylor(double _x)
{
	int N_max = 10;
	double S_N = 0;

	for (int k = 0; k < N_max; k++)
		S_N = S_N + pow(-1, k) * pow(_x, 2 * k + 1) / factorial(2 * k + 1);
	// [TODO] add your algorithm here

	return S_N;
}


// Taylor series approximation for sin(x) (input unit: [deg])
double sindTaylor(double _x)
{
	_x = PI * _x / 180;
	int N_max = 10;
	double S_N = 0;

	for (int k = 0; k < N_max; k++)
		S_N = S_N + pow(-1, k) * pow(_x, 2 * k + 1) / factorial(2 * k + 1);
	// [TODO] add your algorithm here

	return S_N;

	// [TODO] add your algorithm here
}

double cosTaylor(double _x)
{
	int N_max = 10;
	double S_N = 0;

	for (int k = 0; k < N_max; k++)
		S_N = S_N + pow(-1, k) * pow(_x, 2 * k) / factorial(2 * k);
	// [TODO] add your algorithm here

	return S_N;
}

double expTaylor(double _x)
{
	int N_max = 10;
	double S_N = 0;

	for (int k = 0; k < N_max; k++)
		S_N = S_N + pow(_x, k) / factorial(k);
	// [TODO] add your algorithm here

	return S_N;
}


// power fuction
double power(double _x, int N)
{
	double temp = _x;
	for (int i = 0; i < N; i++)
	{
		_x = _x * temp;
	}
	return _x;
	// [TODO] add your algorithm here
}


double deg2rad(double _x)
{
	return _x * PI / 180;
}

 

 

Main file

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define		PI		3.14159265358979323846264338327950288419716939937510582

#include"../../include/myNP_tutorial.h"


int main(int argc, char* argv[])
{

	double x = PI / 3;

	double S_N = 0;

	/*===== Select the function to call =====*/
	S_N = sinTaylor(x);

	printf("\n\n");
	printf("=======================================\n");
	printf("    sin( %f[rad] ) Calculation   \n", x);
	printf("=======================================\n");
	printf("   -  My     result = %3.12f    \n", S_N);
	printf("   -  Math.h result = %3.12f    \n", sin(x));
	printf("   -  absolute err. = %3.12f    \n", S_N - sin(x));
	printf("=======================================\n");


	S_N = sindTaylor(60);

	printf("\n\n");
	printf("=======================================\n");
	printf("    sin( %f[deg] ) Calculation   \n", x);
	printf("=======================================\n");
	printf("   -  My     result = %3.12f    \n", S_N);
	printf("   -  Math.h result = %3.12f    \n", sin(x));
	printf("   -  absolute err. = %3.12f    \n", S_N - sin(x));
	printf("=======================================\n");

	S_N = cosTaylor(x);

	printf("\n\n");
	printf("=======================================\n");
	printf("    cos( %f[deg] ) Calculation   \n", x);
	printf("=======================================\n");
	printf("   -  My     result = %3.12f    \n", S_N);
	printf("   -  Math.h result = %3.12f    \n", cos(x));
	printf("   -  absolute err. = %3.12f    \n", S_N - cos(x));
	printf("=======================================\n");

	S_N = expTaylor(x);

	printf("\n\n");
	printf("=======================================\n");
	printf("    exp( %f[deg] ) Calculation   \n", x);
	printf("=======================================\n");
	printf("   -  My     result = %3.12f    \n", S_N);
	printf("   -  Math.h result = %3.12f    \n", exp(x));
	printf("   -  absolute err. = %3.12f    \n", S_N - exp(x));
	printf("=======================================\n");


	system("pause");
	return 0;
}